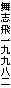
下の図の説明
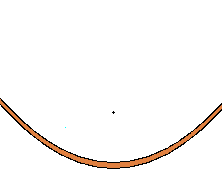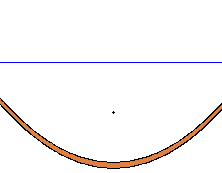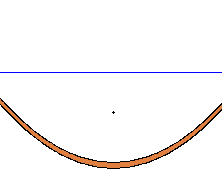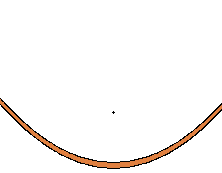
３本の平行線を横に長く等間隔に引きます。
１本ずつ名前をつけます。１番上が y = a の線、真ん中が y = 0 、下が y = -a
これらの直線に垂直に交わる直線を引いて x = 0 の線とします。
x = 0 の線と y = a の線が交わる点を f とします。この点が放物線が完成した時の焦点となります。
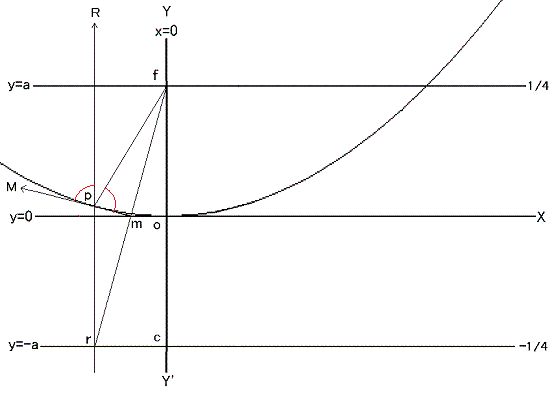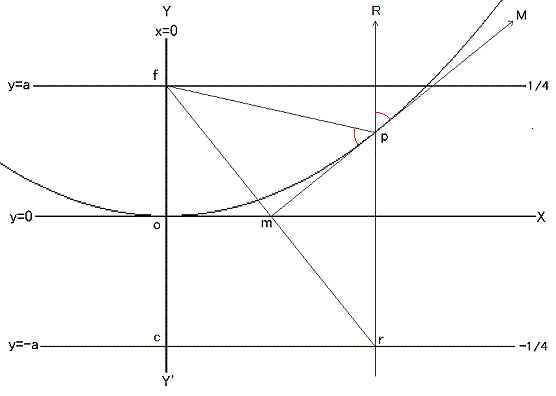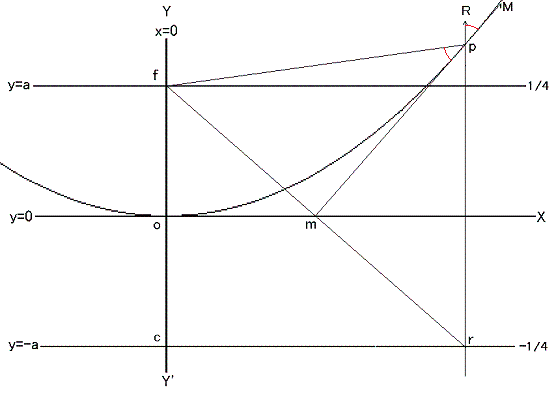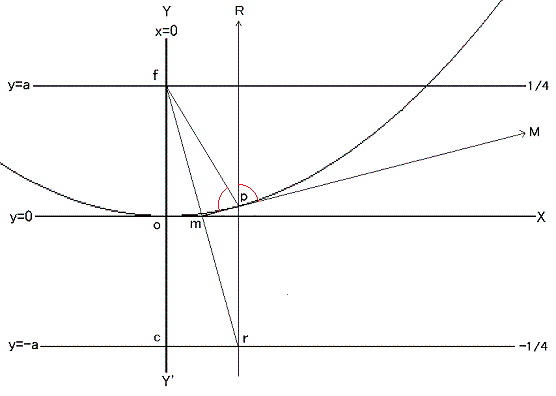つぎに y = -a 線上の任意（勝手）な所に点 r を決めてください。そこからこの直線( y = -a )に垂直に直線を引きます。
f と r を結び線 f r を引き、その垂直２等分線と先ほど r から引いた垂線との交点を p とします。
r 点を y = -a 線の上を滑らして左右すると p 点も動いてその軌跡は放物線になります。
この放物線は a = 0.25 と決めて y = x2 を描いた曲線と合同です。（縦軸と横軸は同じピッチにしてください）
図で f p = p r であり、また 角 f p m = 角 R p M です。（証明は数学の復習のおつもりで各自でどうぞ）
また直線 m M は放物線の p 点に於ける接線です。（これは微分の応用で確かめられます）
この放物線の内面が鏡であれば、焦点 ｆ から出た電波は皆 同一の距離を進むので波面が揃って軸方向へ進みます。
軸方向の遠方Ｒから放物線内面に当たった電波は焦点に集中します。軸に対して斜めだと集中しません。
放物線の軸（ x = 0 の線）を軸にして回転させることを、イメージしてください。そのお椀型が回転放物面（パラボロイド）です。
パラボラアンテナの反射体には円形はじめ様々な形がありますが、この回転放物面の焦点に近い部分を切り取ったものです。【この部分切り取りを私は「剪定」と言います】
だそく
パラボラアンテナ反射鏡の背面は実際には支持構造物ががっちり組み付けられています。これが無く鏡面だったら
真後ろ Y' 方向から来た電波は反射してあたかも焦点 f から放射したように拡散します。
逆に焦点 f に向かって背後から集中する電波があれば、真後ろの Y' 方向にビームになって直進します。
このあと話題が『副反射鏡』へと進みます。
副反射鏡
普通の通信用、レーダー用ならば不必要なのですが、EHF（ミリ波）など波長が短くなると焦点と機器間の伝送が難しくなります。
また、電波望遠鏡では到来する電波が波長も偏波面も種々雑多です。観測内容に合わせた受信装置に入れ替える必要があります。
それらには、焦点がお椀の向こう側ではあたかも別世界のように不便です。そこで手の届く所に焦点を持ってきます。
最初の図で y = -a の直線をY軸上−∞に中心を持つ円の弧であるとイメージします。その時点から放物線は双曲線に変わります。
円の中心を b と名付けます。b を−∞からY軸上を滑らせて引き寄せます。( 0 , -a ) 点 c はそのまま動かしません。円の半径が小さくなります。
y = -a は、既に直線でなくなったのだから名前を 弧b と呼びます。
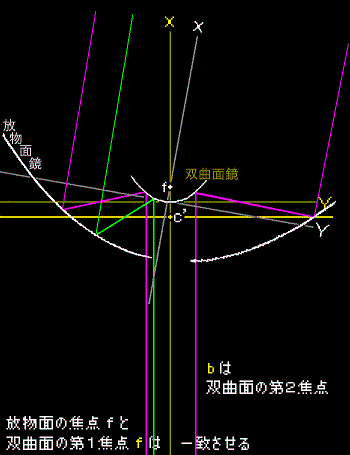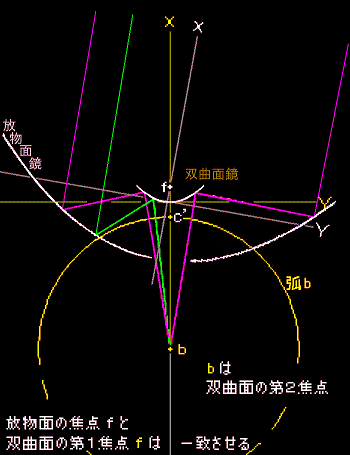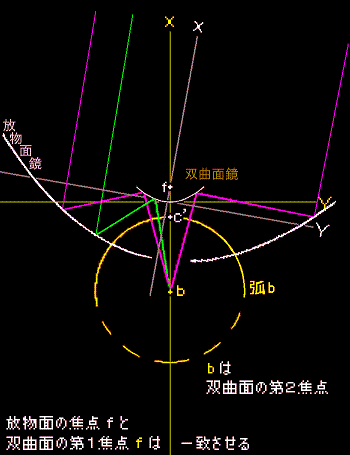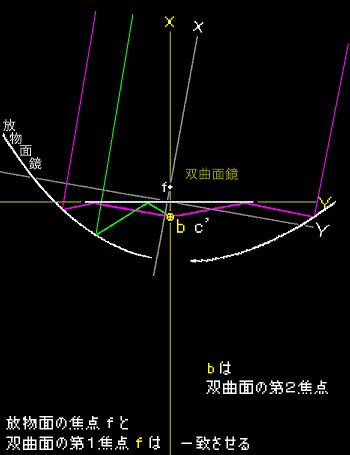
b を近づけるにしたがって元の放物線は開いた形に変わります。放物線ではなく双曲線となりました。 ｆ はこの双曲線の第１の焦点、b が第２の焦点となります。
放物面鏡には双曲面鏡（副反射鏡）の軸を中心に必要な大きさの穴を開けます。第２ の焦点 b は手元の扱いやすい位置になるように双曲面鏡の焦点距離を決めます。
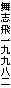
パラボラ開口面積を衛星方向に垂直な面に投影すると、有効面積は凡そ８０％（約−２ｄB）
わざわざ非対称形にしたのは、取付易く、雨水、雪、埃が付かない！ その代償が２ｄB、安い！
